https://www.acmicpc.net/problem/9251
9251번: LCS
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net
두 수열이 주어졌을때, 모두의 부분 수열이 되는 수열중 가장 긴 것을 찾아서 길이를 구하는게 문제의 목표이다.
해당 문제는 부르트포스 방법으로 문제를 해결 할 수 있으나 문자열의 길이가 N, M 일때 시간복잡도가 O(NM)이 걸린다.
하지만 다이나믹 프로그래밍을 적용하여 풀면 O(NM)으로 문제를 해결 할 수 있다.
1) 브루트포스 방식으로 문제 접근
1. 문자열1에서 부분수열을 구하는 시간복잡도는 O(2^N) 이다. 왜냐하면 해당 부분문자가 있는경우와 없는경우로 나뉘기 때문입니다.
ACAYKP의 부분수열을 만드는 예 입니다.
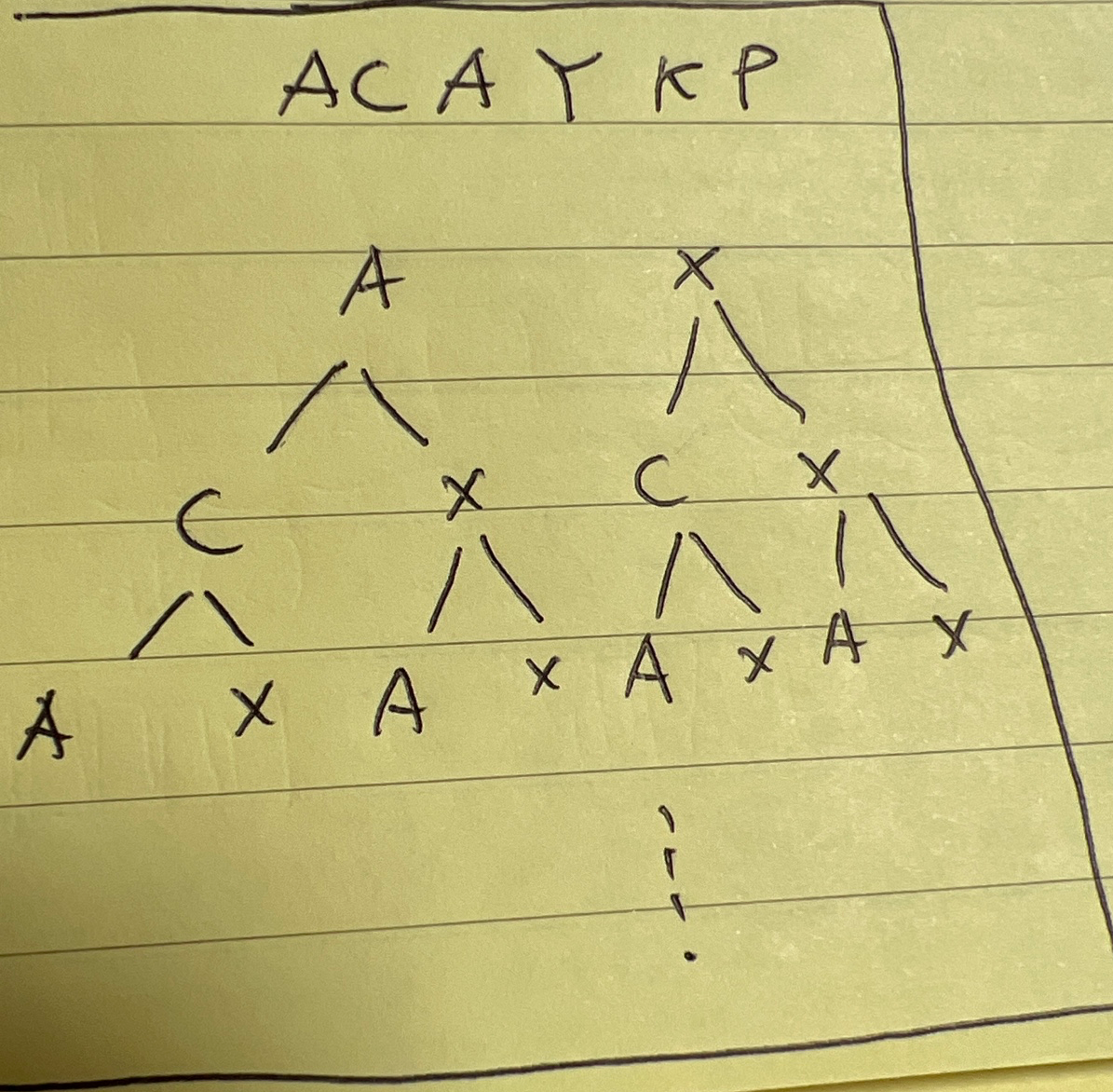
2. 문자열1에서 구한 부분수열을 문자열2와 비교하는 시간복잡도는 O(M)이다.
따라서 최악의 경우 브루트포스로 문제를 풀경우 O(M*2^N) 가 나온다. 따라서 브루트포스 방식으로는 해당 문제를 해결 할 수 없다.
2) 다이나믹 프로그래밍 방식으로 문제 접근
1. 문자열 ACAYKP와 CAPCAP가 주어졌을때 최대길이는 문자열 인덱스를 1을 줄인 ACAYK와 CAPCA의 문자열의 길이의 +1의 값과 같다.
2. 만약 같지않다면 ACAYK와 CAPCA에서 max ((ACAYK, CAPC), (ACAY, CAPCA))로 구할 수있다.
즉, SubProblem은 위와 같은 조건으로 만족이 됩니다.
string1은 문자열, string2는 문자열, i는 string1의 인덱스, j는 string2의 인덱스 라고 할때,
if string1[i] == string2[j]
dp[i][j] = dp[i-1][j-1] +1
else
dp[i][j] = max(dp[i-1][j], dp[i][j-1]
로 값을 표현 할 수 있다.
테스트케이스인 ACAYKP와 ACPCAK의 dp테이블을 나타내 보았습니다.
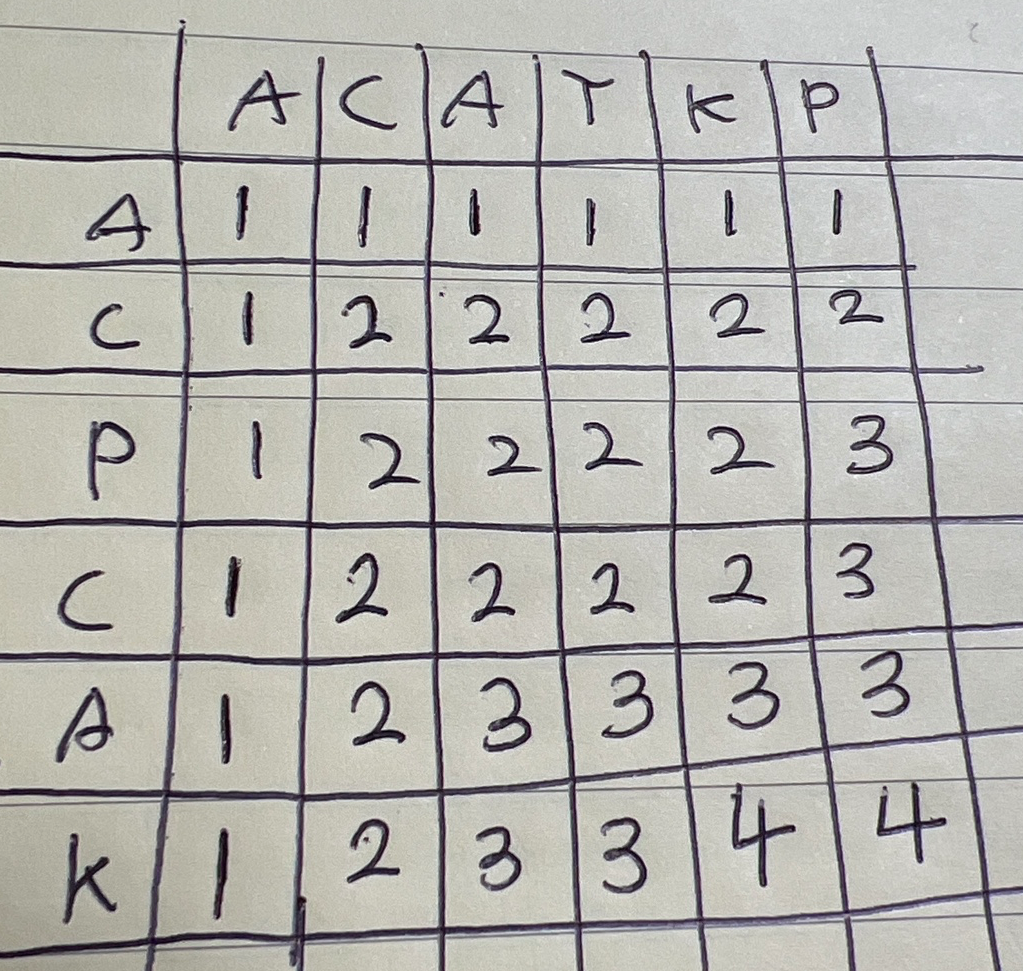
str1 = str(input())
str2 = str(input())
length1 = len(str1)
length2 = len(str2)
def LCS(i,j):
if length1 > i >= 0 and length2 > j >=0:
if str1[i] == str2[j]:
return LCS(i-1,j-1) + 1
else :
return max(LCS(i-1, j), LCS(i, j-1))
else:
return 0
print(LCS(length1-1, length2-1))'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 2156번 : 포도주 시식 (0) | 2023.07.14 |
|---|---|
| [백준] 1010번 : 다리 놓기 (0) | 2023.07.13 |
| [백준] 12865번 : 평범한 배낭 (2) | 2023.07.13 |
| [백준] 1463번 : 1로 만들기 (2) | 2023.07.13 |
| [백준] 14500번 : 테트로미노 (0) | 2023.07.04 |
