https://www.acmicpc.net/problem/11066
11066번: 파일 합치기
소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본
www.acmicpc.net
해당 문제는 브루트포스 알고리즘으로 문제를 해결할 경우 시간복잡도가 O(!(N-1))으로 문제를 해결 할 수 있습니다.
예를들어 40, 30, 30, 50 이라는 수가 주어져 있을때
1. 40, (30,30,50) 에서 더해지는 경우
2. (40,30), (30,50) 에서 더해지는 경우
3. (40,30,50),50 에서 더해지는 경우
숫자가 N개 일때 N-1 경우의 수가 발생한다. 즉 N-1 * N-2* N-3 ... 와 같은 시간복잡도가 발생하여 O(!(N-1)) 이라는 시간복잡도가 발생합니다. 하지만 해당 문제를 메모리제이션 기법을 활용하여 중복된 연산을 제거 하여 O(N^2) 시간복잡도로 문제를 해결 할 수 있습니다.
예를들어 3번째 경우의 수인 (40,30,50)는 (40,30) +50 혹은 40+(30,50) 에서 오는걸 알 수 있습니다. 경우의 수 2번에서 (40,30)과 (30,50)과 동일한 중복문제가 발생한다는것을 알 수 있습니다. 해당 연산을 메모리제이션 하여 최적화 할 수 있습니다.
따라서 해당 문제를 메모리 제이션 할 수 있는 dp 테이블을 생성하는데 dp[i][j]는 i번째 수부터 j번째 수까지의 합을 저장하는 테이블을 작성합니다. (40,30,50) 을 구하는 과정은 dp[0][2] = min(dp[0][1] + dp[2][2], dp[0][0]+dp[1][2] ) 라는 점화식이 세워 집니다.
dp[0][1]은 2번 경우의수인 (40,30)을 계산한 값이고, dp[1][2]도 2번 경우의수인 (30,50)을 계산한 값입니다.
dp[i][j]를 구하려면 N-1의 경우의 수가 발생하지만 메모리제이션 기법으로 2차원 배열을 채워나가는 O(n^2)의 시간복잡도를 갖을 수 있습니다.
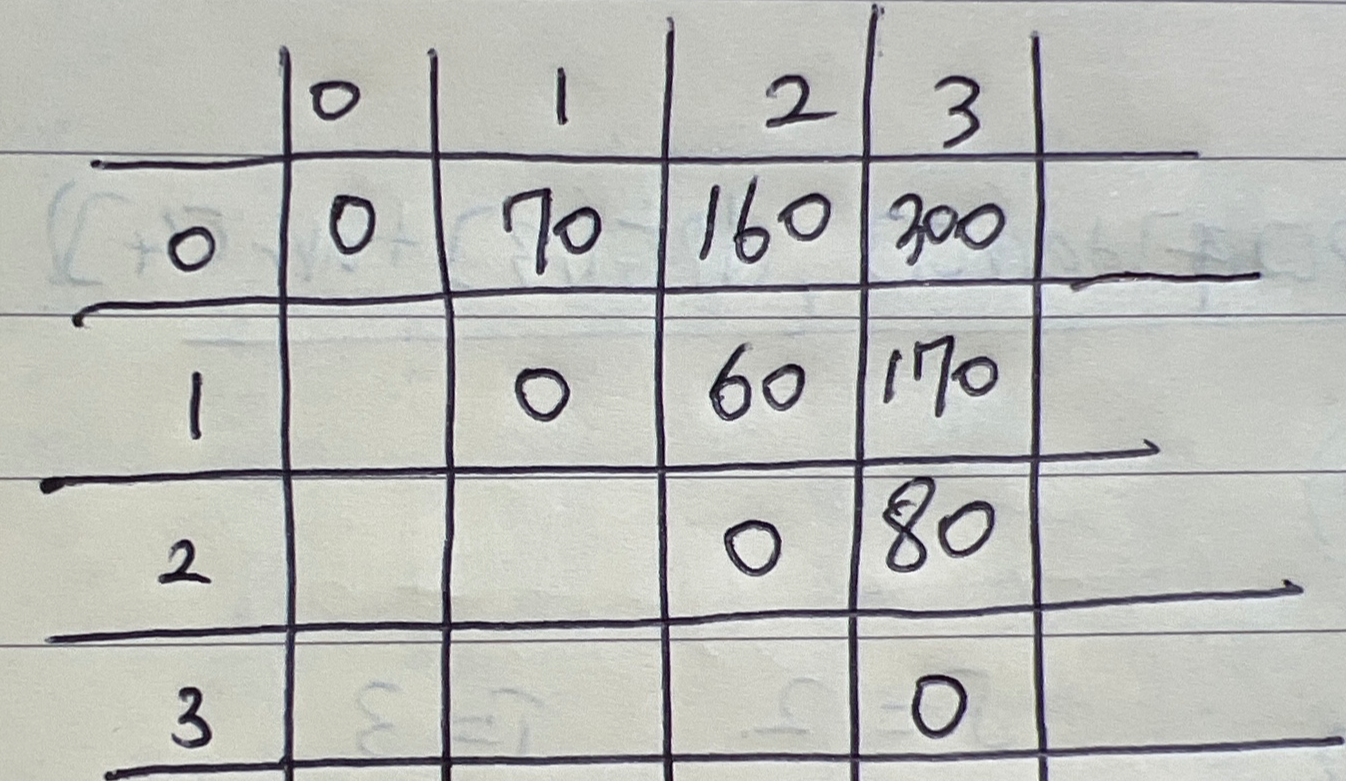
테스트 케이스 40, 30, 30, 50 메모리제이션 테이블 표
T = int(input())
for _ in range(T):
K = int(input())
arr = list(map(int, input().split()))
dp = [[0 for _ in range(K)] for _ in range(K)]
for j in range(1, K):
for i in range(j-1, -1 , -1):
minvalue = int(10e9)
for k in range(j-i):
minvalue = min(minvalue, dp[i][i+k] + dp[i+k+1][j])
dp[i][j] = minvalue + sum(arr[i:j+1])
print(dp[0][K-1])'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 11053번 : 가장 긴 증가하는 부분수열 (0) | 2023.07.16 |
|---|---|
| [백준] 2293번 : 동전 1 (0) | 2023.07.16 |
| [백준] 1916번 : 최소비용 구하기 (0) | 2023.07.15 |
| [백준] 1753번 : 최단경로 (0) | 2023.07.15 |
| [백준] 1520번 : 내리막길 (2) | 2023.07.15 |